One of my recent hobby is to think of fun math problems to encourage our 6-year-old daughter to play with the virtue of numbers. At the moment she knows of multiplication and division between pairs of 1-digit integers as the most advanced topic to her.
When I talked with her over 9×9 multiplication table—a standard material for elementary math in my country—, I realized that any 2-digit integers converge to an 1-digit integer after repeatedly applying a certain operation. The operation is quite simple; take the first and second digits and multiplying them. For example, the operation, let us call it the digit multiplication hereafter, transform 23 into 2×3 = 6, 54 to 5×4 = 20, and so on.
Let us quickly recap that any 2-digit integers eventually converge to 1-digit with this. A 2-digit integer is represented as 10a+b with a, b = 1, 2, …, 9. Then, the digit multiplication converts 10a+b to ab. It is straightforward to see following two properties of the digit multiplication. First, the resultant ab is bounded from both sides as 1 ≤ ab ≤ 81. Second, the digit multiplication always returns output smaller than its input: the difference is negative as ab – (10a+b) = (a-1)b – 10a ≤ 10(a-1) – 10a = -10 (the equality holds iff a = 1). These two properties ensure that the digit multiplication transforms any 2-digit integer into 1-digit after some iterations, at most 8 times (a rough estimation).
Now if we take the number of iterations required to reduce a 2-digit integer into an 1-digit as its "distance" to any 1-digits, we can find the most distant 2-digit among 10 to 99. To find the extreme one, should we apply the digit multiplication for several times until all the results become less than 10? Definitely not! Instead, we apply the digit multiplication only once and then draw a network between numbers.
The whole space of operating the digit multiplication is represented as 10 directed trees between numbers in which a directed edge is drawn from input to output such as 23 → 6 and 54 → 20 and the roots of which are 0 to 9, i.e., the destinations. Following visualizations tell us how these trees look like:


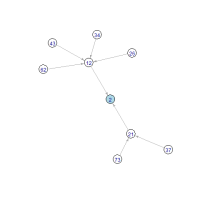
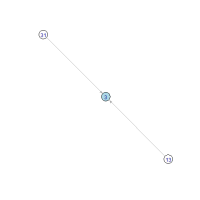
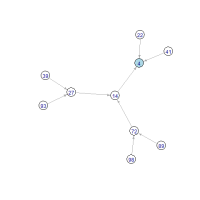


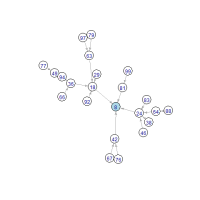

Apparently the trees of root 0, 6, and 8 are the largest ones. By contrast, the trees of root 1, 3, 7, and 9 are the smallest ones, surrounded by only a few primes (except 33 and 91). We seem to come to the roots in a few steps wherever we start at and the most distant one may be in the trees of 0, 6, or 8.
The answer to the most-distant-one question becomes crystal clear when we plot the 2-digit integers and its distance to the nearest root as follows:

The answer is 77! Among 10 to 99, only 77 requires 4 steps to come to 8, via 77 → 49 → 36 → 18 → 8. Now dad keeps this new piece into his “fun-math-fact” list to show it to daughters someday…
Below is the script to reproduce the figures:
library(dplyr)
library(ggplot2)
library(ggthemes)
library(igraph)
library(glue)
# Set the data
x <- 0:99
y <- ifelse (x < 10, NA, (x %/% 10) * (x %% 10))
df <- data.frame("x" = x, "y" = y)
# Create a directed graph from the data
g <- graph.data.frame(df %>% filter(!is.na(y)), directed = TRUE)
# Find 10 components (directed & rooted trees) in g
c <- components(g)
# Plot each tree
for (cid in 1:10) {
cc <- induced.subgraph(g, vids = V(g)[c$membership == cid], impl = "copy_and_delete")
png(glue("./R/plot_component{cid-1}.png"))
plot.igraph(x = cc,
vertex.color = ifelse(degree(cc, mode = "out") == 0, "light blue", "white"),
vertex.label.family = "sans",
edge.arrow.size = 0.5)
dev.off()
}
# Plot the distance from leaves to the nearest root (1-digit number)
d <- distances(graph = g, v = V(g)[1:90], to = V(g)[91:100], mode = "out")
dmin <- apply(X= as.matrix(d, ncol = 9), MARGIN = 1, FUN = min)
ggplot (data = data.frame(x = as.integer(names(dmin)), y = dmin),
aes(x = x, y = y, color =y)) +
geom_segment(aes(x = x, y = 0, xend = x, yend=y), size = 1.2) +
geom_point(size=3, color = "grey40") +
xlab("2-digit number") +
ylab("distance to the nearest 1-digit number") +
scale_color_continuous(low = "grey", high = "#0072B2") +
guides(color = FALSE) +
theme_minimal(base_size = 15)